Voltage, current, and charge control
The collector–emitter current can be viewed as being controlled by the base–emitter current (current control), or by the base–emitter voltage (voltage control). These views are related by the current–voltage relation of the base–emitter junction, which is just the usual exponential current–voltage curve of a pn junction (diode).
The physical explanation for collector current is the amount of minority-carrier charge in the base region. Detailed models of transistor action, such as the Gummel Poon model, account for the distribution of this charge explicitly to explain transistor behavior more exactly. The charge-control view easily handles phototransistors, where minority carriers in the base region are created by the absorption of photons, and handles the dynamics of turn-off, or recovery time, which depends on charge in the base region recombining. However, because base charge is not a signal that is visible at the terminals, the current- and voltage-control views are generally used in circuit design and analysis.
In analog circuit design, the current-control view is sometimes used because it is approximately linear. That is, the collector current is approximately βF times the base current. Some basic circuits can be designed by assuming that the emitter–base voltage is approximately constant, and that collector current is beta times the base current. However, to accurately and reliably design production BJT circuits, the voltage-control (for example, Ebers Moll) model is required. The voltage-control model requires an exponential function to be taken into account, but when it is linearized such that the transistor can be modelled as a trans-conductance, as in the Ebers Moll model, design for circuits such as differential amplifiers again becomes a mostly linear problem, so the voltage-control view is often preferred. For trans-linear circuits, in which the exponential I–V curve is key to the operation, the transistors are usually modelled as voltage controlled with trans-conductance proportional to collector current. In general, transistor level circuit design is performed using SPICE or a comparable analogue circuit simulator, so model complexity is usually not of much concern to the designer.
Turn-on, turn-off, and storage delay
The Bipolar transistor exhibits a few delay characteristics when turning on and off. Most transistors, and especially power transistors, exhibit long base storage time that limits maximum frequency of operation in switching applications. One method for reducing this storage time is by using a baker clamp.
Transistor 'alpha' and 'beta'
The proportion of electrons able to cross the base and reach the collector is a measure of the BJT efficiency. The heavy doping of the emitter region and light doping of the base region cause many more electrons to be injected from the emitter into the base than holes to be injected from the base into the emitter. The common emitter current gain is represented by βF or hfe; it is approximately the ratio of the DC collector current to the DC base current in forward-active region. It is typically greater than 100 for small-signal transistors but can be smaller in transistors designed for high-power applications. Another important parameter is the common base current gain, αF. The common-base current gain is approximately the gain of current from emitter to collector in the forward-active region. This ratio usually has a value close to unity; between 0.98 and 0.998. Alpha and beta are more precisely related by the following identities (NPN transistor):
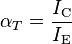






No comments:
Post a Comment