NODAL ANALYSIS

After simulating circuits for some time, I began to ask myself - how does this SPICE program work? What mathematical tricks does the code execute to simulate complex electrical circuits described by non-linear differential equations? After some searching and digging, some answers were uncovered. At the core of the SPICE engine is a basic technique called Nodal Analysis. It calculates the voltage at any node given all resistances (conductances) and current sources of the circuit. Whether the program is performing DC, AC, or Transient Analysis, SPICE ultimately casts its components (linear, non-linear and energy-storage elements) into a form where the innermost calculation is Nodal Analysis.

WHAT IS NODAL ANALYSIS?

Kirchoff discovered this: the total current entering a node equals the total current leaving a node! And, these currents can be described by an equation of voltages and conductances. If you have more than one node, then you get more than one equation describing the same system (simultaneous equations). The trick now is finding the voltage at each node that satisfies all of the equations simultaneously.

Circuit Example Here’s a simple circuit example.

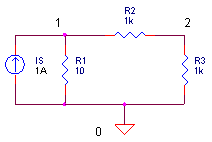
Another way of stating the KC Law is this: the sum of currents in and out of a node is zero. This makes writing nodal equations a piece of cake. The two equations for the two circuit nodes look like this.

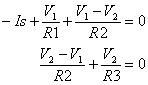
Because our mission is to calculate the node voltages, let’s reorganize the equations in terms of V1 and V2.

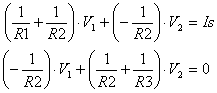
So here sit V1 and V2 in the middle of two different equations. The trick is finding the values of V1 and V2 that satisfy both equations. But how?

SOLUTION #1 – WORK THE EQUATIONS

Just roll up your sleeves and solve for V1 and V2. Before we begin we’ll make bookkeeping easy by writing the resistors in terms of total conductance: G11 = 1/R1 + 1/R2, G12 = -1/R2, G21 = -1/R2 and G22 = 1/R2+1/R3. The system equations now look like this.

First, solve the second equation for V1

Then, stick this into the first equation and solve for V2

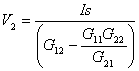
Okay, it’s a little messy, but we’ve got V2 described by circuit conductances and Is only! After V2 is calculated numerically, stick it back into V1 = – G22 ∙V2 / G21 and there you have it, circuit voltages V1 and V2 that satisfy both system equations.

SOLUTION #2 – THE MATRIX

Solution #1 looks reasonable for simple circuits, but what about medium or large circuits? The bookkeeping of terms spins out of control quickly. What’s needed is a more methodical and efficient solution: Enter the Matrix. Here’s the set of nodal equations written in matrix form.

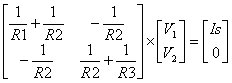
Or, in terms of total conductances and source currents

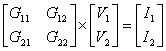
Treating each matrix as a variable, you can write

G ∙ v = i

In the matrix world, you can solve for a variable (almost) like any other algebraic equation. Solving for v you get

v = G^-1∙ i

Where G^-1 is the matrix inverse of G. ( 1 / G does not exist in the matrix world.) This equation is the central mechanism of the SPICE algorithm. Regardless of the analysis – AC, DC, or Transient – all components or their effects are cast into the conductance matrix G and the node voltages are calculated by v = G^-1∙ i , or some equivalent method.